Informações básicas
Wilensky, U. (1997). NetLogo Party model. http://ccl.northwestern.edu/netlogo/models/Party. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
Acesso Modeling Commons
Analisado por Lênio de Souza Oliveira
Última atualização: setembro/2023
Visão geral
Este modelo foi formulado para explorar questões de segregação entre grupos de homens e mulheres em uma festa. Dessa maneira, a depender da quantidade de pessoas do sexo oposto no grupo e da tolerancia global do aplicado no modelo, o festeiro fica (ou não) mais desconfortável e troca de grupo.
Entidades, variáveis de estado e escalas
Modelo composto por apenas dois (2) agentes: os homens, representados pela cor azul; e as mulheres, representadas pela cor amarela. E o ambiente onde os agentes interagem é formado por grupos de homens e mulheres de números variados e que trocam entre si (ou não) quando estão insatisfeitos no grupo, a depender da tolerância aplicada.
Visão geral do processo e programação dos eventos
Os processos do modelo se dão a partir da necessidade das trocas de grupo. Essas trocas ocorrem a partir da “felicidade” de se estar no grupo, dependendo do número de pessoas do sexo oposto que fazem parte desse grupo e da tolerância global. Dessa forma, se a tolerância estiver em níveis mais baixos, a “felicidade” de se estar no grupo também será baixa se o número de pessoas do sexo oposto for maior do que o tolerável.
Conceitos de Design
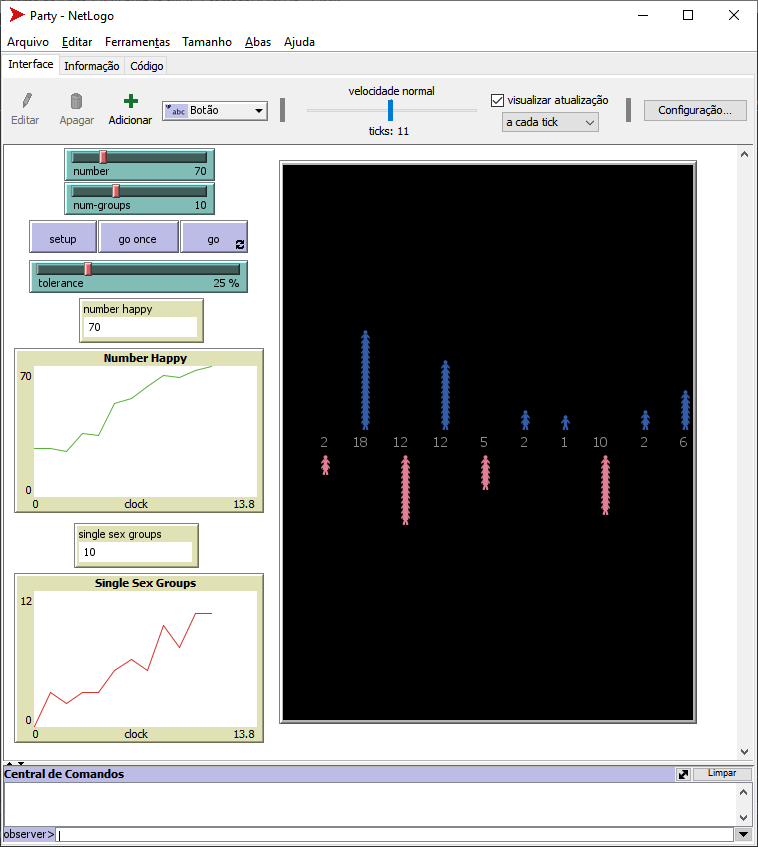
Os principais resultados que emergem por meio do modelo são: 1) o número de pessoas felizes; 2) o número de grupos compostos por apenas um sexo; e 3) o número de grupos com integrantes de ambos os sexos. Tais resultados dependem da manipulação do parâmetro referente ao número de agentes no modelo, do número de grupos no modelo e da tolerância padrão do modelo.
Os agentes apresentam comportamentos adaptativos a partir do momento em que se faz a troca de grupo para que se sintam mais felizes em seus respectivos grupos, tomando decisões a partir da tolerância com o número de pessoas do sexo oposto no grupo.
Neste modelo os agentes não apresentam aprendizado e predição.
A percepção é importante neste modelo, pois é a partir dela que os agente podem ou não trocar de grupo para se sentir mais felizes.
O modelo foi baseado no mecanismo de segregação, dessa forma a interação entre os agente é mediada pela troca de grupos na busca por mais felicidade a partir do número de pessoas do mesmo sexo no grupo.
O modelo apresenta coletivos, uma vez que se trata de formação de grupos, onde as características de variedade de gênero do grupo podem influenciar ou não a tomada de decisão de cada agente do grupo em buscar um novo grupo.As observações a serem consideradas são os gráficos que representam a flutuação de pessoas felizes e grupos formados por apenas um gênero e os dados que apresentam o número final de pessoas felizes e os grupos formados por apenas um gênero.
Detalhes
Inicialização
O modelo apresenta inicialização bastante customizável, podendo selecionar o número de pessoas (que varia de 0 a 300), o número de grupos no início da representação (que varia de 5 a 20) e a tolerância (que varia de 0 a 99). A partir da escolha destas 3 variáveis, o modelo forma os grupos de maneira aleatória.
Submodelos
Atualizar felicidade
Primeiro, ocorre a contagem de quantas tartarugas estão no grupo:
let total count turtles-here
Depois, a contagem de quantas tartarugas tem a mesma cor que ela:
let same count turtles-here with [color = [color] of myself]
Após isso, é feito uma contagem do sexo aposto a partir da subtração do total de tartarugas do grupo pelo número de tartarugas de cores igual a ela:
let opposite (total - same)
A tartaruga estará feliz no grupo se o número de tartarugas do sexo oposto não excede sua tolerância:
set happy? (opposite / total) <= (tolerance / 100))
Sair se estiver infeliz
Se a tartaruga não estiver feliz no grupo ela vai virar para a esquerda ou para direita aleatoriamente e sair do grupo.
Achar novos grupos
Faz com que a tartaruga procure novos grupos para integrar.
Referências
Resnick, M. & Wilensky, U. (1998). Diving into Complexity: Developing Probabilistic Decentralized Thinking through Role-Playing Activities. Journal of Learning Sciences, Vol. 7, No. 2. http://ccl.northwestern.edu/papers/starpeople/
Schelling, T. (1978). Micro-motives and Macro-Behavior. New York: Norton